Precipitaciones
Storyboard 
Formación de gotas, dinámica de formación y caída a una velocidad dependiente del radio.
ID:(554, 0)
Gotas de lluvia
Imagen 
Las gotas de lluvia son esféricas. Sin embargo sobre una superficie como el vidrio forman, causado por la tensión superficial, gotas aplanadas.

Gotas de lluvia
ID:(3112, 0)
Lluvia torrencial
Imagen 
En zonas de alta humedad relativa y alta temperatura, como los bosques tropicales, se pueden formar lluvias de alta intensidad:

Lluvia torrencial
ID:(3113, 0)
Caída de lluvia
Descripción 
La conensación de agua al ocurrir la decompresión adiabatica lleva a que las moleculas de agua en el aire tiendan a formar gotas.
Dichas gotas tienden a caer generando una corriente laminar que genera una fuerza de resistencia proprocional a la velocodad de caida y al radio de la gota.
Para gotas muy chicas la velocidad e caida es tan lenta que practicamente permanecen suspendidas. Solo si logran formarse gotas de mas de diez micrones la velocidad es suficientemente grande para crear lluvia.
ID:(44, 0)
Flujo de agua condensada
Ecuación 
Si se multiplica la concentración del agua condensada
| j_d = \Delta c v |
ID:(4875, 0)
Formación de gotas de lluvia
Imagen 
Para comenzar a formar las gotas de lluvia se requiere de agua condensada, es decir moléculas de agua en estado liquido. Eso es moléculas con poca energía de modo que al colisionar con otras se quedan adheridas formando una micro gota.
El proceso de crecimiento continua tanto por adhesión de nuevas moléculas a gotas ya existentes o por fusión de micro gotas que colisionan y forman gotas mas grandes.
El proceso continua hasta que el tamaño de las gotas es tan grande que su velocidad de caída crece y hace que estas abandonen la zona de crecimiento precipitándose a la tierra.
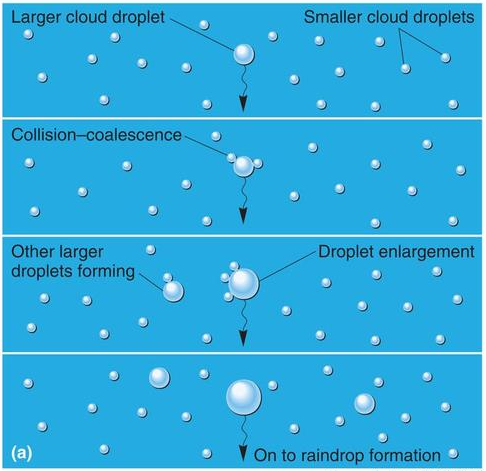
Gotas de lluvia
Gotas que alcanzan a crecer mucho están sujetas a fraccionarse en gotas de menor tamaño. Esto ocurre por las turbulencias en el proceso de caída que hacen que la gota oscile de una forma esférica a la de un disco. Si la tensión superficial lleva a que el disco termine como un toroide este se fracciona en multiples gotas chicas.
ID:(9704, 0)
Fuerza de Stokes
Ecuación 
La resistencia se define en función de la viscosidad del fluido y la velocidad de la esfera de la siguiente manera:
| F_v = b v |
Stokes calculó explícitamente la resistencia experimentada por la esfera y determinó que la viscosidad es proporcional al radio de la esfera y su velocidad, lo que lleva a la siguiente ecuación para la resistencia:
ID:(4871, 0)
Velocidad de caida de gotas
Ecuación 
La fuerza que resiste la caida de una gota se puede describir con la ley de fuerza de Stokes:
| F_v =6 \pi \eta r v |
la que se opone a la gravedad
que tienden a acelerar la gota. Si se igualan ambas fuerzas se puede estimar la velocidad a la que la gota tienden a caer
| v_g =\displaystyle\frac{2 r ^2 \rho g }{9 \eta } |
En el caso de lluvia las gotas tienen tipicamente 0.5 mm de radio y como la densidad del agua es 1 g/cm3, la viscosidad del aire 1.8E-5 Pa s y la aceleración gravitacional 9.8 m/s2 se tiene una velocidad de 30.3 m/s.
> *La velocidad de caída de las gotas de lluvia es constante debido a la resistencia del aire. Su magnitud puede llegar a ser de varias decenas de metros por segundo.*
Las gotas pueden llegar a tener varios milímetros de radio, sin embargo la velocidad lleva a que la fuerza que ejerce el aire sobre ellas tienda a fragmentarlas con que se reduce nuevamente su radio.
> *Gotas de lluvia de mayor tamaño están expuestas a mayores tensiones por las fuerzas de resistencia del aire lo que lleva a su fragmentación. Por ello las gotas tienden a no superar diámetros de varios milímetros.'
En el caso de neblina los radios son del orden de 2.2 mu por lo que la velocidad es del orden de 5.8E-4 m/s lo que es relativamente lento. En una hora la gota de neblina solo recorrería 2 m por lo que la neblina solo puede 'levantarse' si las gotas continúan creciendo o se evaporan nuevamente.
> *Gotas de neblina tienen velocidades de caída muy pequeñas que en la escala de tiempo de interés pueden ser despreciadas. Por ello se les puede considerar en suspensión significando que la disolución de la neblina se puede dar solo por crecimiento de las gotas (lluvia) o evaporación.*
ID:(4872, 0)
Velocidad relativa de caida
Ecuación 
La velocidad relativa
| v_e = v_g - v_m |
Dado que se puede dar que la velocidad de acenso de las masas de aire (por convección) es mayor a las de caidad de las gotas, se puede dar que literalmente 'llueve para arriba'. Otro fenomeno es el de evaporación. Dependiendo de la humedad relativa por la que atravieza una gota de agua esta puede ganar tamaño o ir evaporandose. En este ultimo caso se vuelve cada vez mas lenta pudiendo en extremo nunca alcanzar el suelo. En otras palabas se tiene lluvia en altura que no llega al suelo.
ID:(4873, 0)
Precipitaciones en función de la latitud (D1+0)
Php 
La humedad relativa en función de la latitud refleja aumentos en las zonas de convección en que las masas de aire ascienden. Esto es en el ecuador y entre las celdas de Ferrel y polres:
Adicionalmente se ve que disminuye en general con la altura lo que se asocia a la generación de precipitaciones y correspondiente reducción de agua en la atmósfera.
ID:(9299, 0)
Precipitaciones en función del tiempo (D0+1)
Php 
La humedad relativa en función de la latitud refleja aumentos en las zonas de convección en que las masas de aire ascienden. Esto es en el ecuador y entre las celdas de Ferrel y polres:
Adicionalmente se ve que disminuye en general con la altura lo que se asocia a la generación de precipitaciones y correspondiente reducción de agua en la atmósfera.
ID:(9306, 0)
Medición de tamaño de gota en neblina
Imagen 
Las gotas de agua contenidas en la neblina son de un tamaño entre fracciones y algunas decenas de micrones:
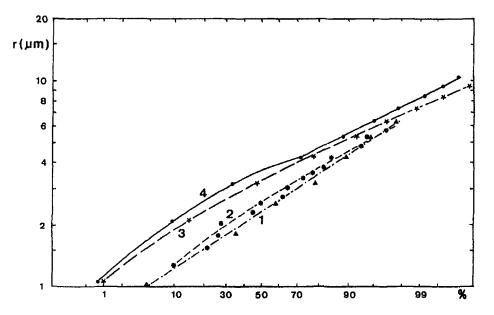
Distribución de gotas de neblina en distintas ubicaciones (Studia geoph. et geod. 41 (1997), 277-296)
Según la gráfica el 50% de las gotas tienen un radio inferior a unos 2.2 mu. Por ello podemos concluir que
> La típica gota de neblina tiene un radio de 2.2 mu
ID:(7815, 0)
Medición de tamaño de gota en lluvia
Imagen 
Las gotas de lluvia son de un tamaño entre fracciones y algunos milímetros:
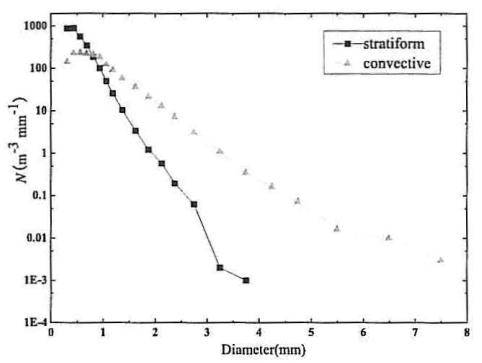
Distribución de gotas de lluvia según origen (Niu, J. Appl. Mcteor., 10 (2010), 632-645)
Según la gráfica, el máximo se encuentra en ambos casos para gotas que tienen un radio de alrededor de 0.5 mm. Por ello podemos concluir que
> La típica gota de lluvia tiene un radio de 0.5 mm
ID:(7816, 0)
Velocidad media de las partículas
Ecuación 
Si se iguala la energía cinética (K) con la energía de una molécula (E) se puede calcular en función de el grados de libertad (f), la constante de Boltzmann (k_B), la temperatura absoluta (T) y la masa de la partícula (m) lo que es la velocidad media de una partícula (\bar{v}) mediante
La energía cinética (K) con la masa de la partícula (m) y la velocidad media de una partícula (\bar{v})
| K =\displaystyle\frac{ m }{2} \bar{v} ^2 |
y la energía de una molécula (E) con el grados de libertad (f), la constante de Boltzmann (k_B) y la temperatura absoluta (T)
| E =\displaystyle\frac{ f }{2} k_B T |
que al igualar dan
| \bar{v} =\sqrt{\displaystyle\frac{ f k_B T }{ m }} |
ID:(4391, 0)
Tiempo de crecimiento de gotas
Ecuación 
Las gotas se van formando por las moléculas de agua que ya condensaron y por ello se adhieren a cualquier otra molécula de agua. Si se calcula la velocidad con que se van agregando las moléculas se puede estimar la relación entre tiempo y radio:
| t =\displaystyle\frac{6 \rho }{ c v M_m } a |
ID:(4877, 0)
