Indicadores
Storyboard 
La presencia de poros es un aspecto fundamental en el comportamiento del suelo. Por un lado, los poros permiten el movimiento del agua y/o la humedad a través de ellos, pero al mismo tiempo comprometen las propiedades mecánicas del suelo.
Por esta razón, es de suma importancia disponer de indicadores que describan la presencia de porosidad y la proporción de agua que contienen, ya que estos indicadores son clave para caracterizar las propiedades hídricas, termodinámicas y mecánicas del suelo.
ID:(365, 0)
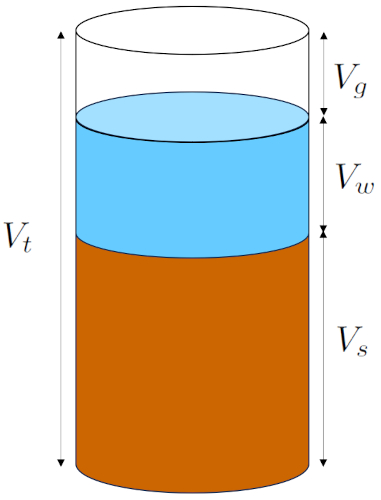
Modelo del volumen solido, agua y gas
Imagen 
En el modelo del suelo, el volumen total ($V_t$) de la muestra se compone de tres partes principales:
• el volumen sólido ($V_s$): Este componente incluye el volumen de todos los granos presentes en la muestra.
• el volumen de agua ($V_w$): Representa el volumen del agua contenida tanto en los microporos como en los macroporos del suelo.
• el volumen de gas ($V_g$): Comprende el volumen de gas o aire contenido en la muestra.
El siguiente diagrama resume esta descripción:
ID:(1642, 0)
Representación de la profundidad efectiva
Nota 
La profundidad efectiva ($D_e$) se refiere a la profundidad que alcanzaría el agua contenida en un volumen de suelo si todo el volumen sólido fuera "removido", como se ilustra en la siguiente imagen:
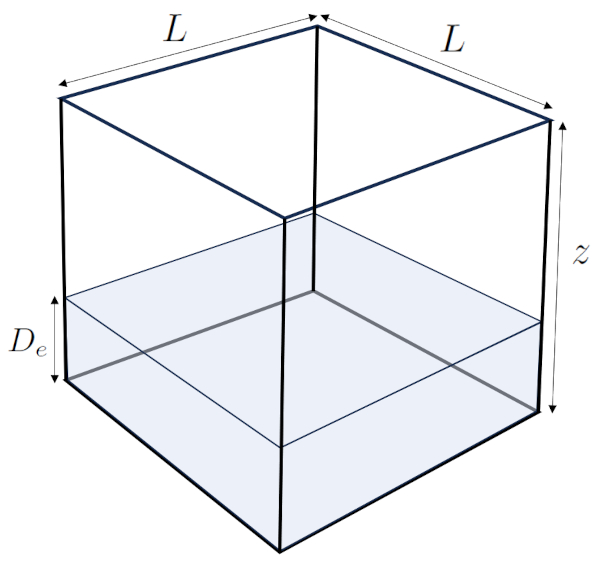
Esta medida proporciona una comprensión intuitiva del agua contenida en el suelo.
ID:(1641, 0)
Modelo de masa solida, agua y gas
Cita 
En el modelo del suelo, la masa total ($M_t$) de la muestra se compone de tres partes principales:
• la masa seca total de la muestra ($M_s$): Este componente incluye las masas de todos los granos presentes en la muestra.
• la masa de agua en el suelo ($M_w$): Representa la masa del agua contenida tanto en los microporos como en los macroporos del suelo.
• la masa del gas en el suelo ($M_g$): Comprende la masa de gas o aire contenido en la muestra (que comparativamente puede considerarse igual a cero, es decir, $M_g\sim 0$).

ID:(2084, 0)
Superficie interna
Ejercicio 
Una de las propiedades distintivas del material particulado, como el suelo, es su superficie interna. Por superficie interna entendemos la suma de todas las superficies de cada uno de los granos. Esta superficie es uno de los factores clave para estudiar el comportamiento de la humedad y la presencia de nutrientes en el suelo.
Al multiplicar la superficie de cada grano por su cantidad, obtenemos la superficie total. Para determinar la superficie de cada grano, es esencial tener en cuenta su forma. Es importante recordar que tanto la arena como el limo se modelan como esferas, mientras que la arcilla se representa como un paralelepípedo recto.
ID:(1540, 0)
