Forma como el viento genera circulación en los océanos
Imagen 
El movimiento de la atmósfera es uno de los principales motores del movimiento de las masas de agua de los océanos. Aun cuando no es un proceso demasiado eficiente. El viento logra que las capas del agua se desplacen a aproximadamente 2% de su velocidad. Sin embargo la inercia de la masa del agua hace que las corrientes persistan en el tiempo.
La circulación en mar se puede describir mediante grandes torbellinos que se forma en cada océano:
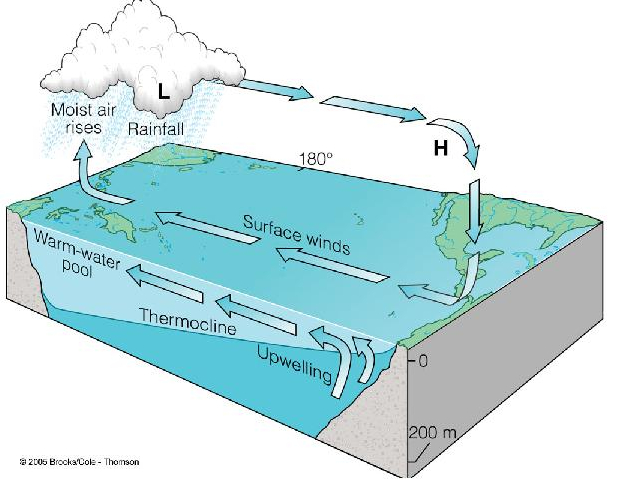
Circulación en el mar
Las circulaciones oceánicas tampoco son totalmente estables. Existen situaciones en que los torbellinos se desplazan como ha ocurrido con aquel que baña las costas de Noruega con agua cálida del caribe creando inviernos mas fríos en las regiones escandinavas y en Europa en general.
ID:(77, 0)
Superposición de las corrientes atmosféricas y oceánicas
Imagen 
Si observamos los patrones que se dan en las corrientes oceánicas veremos nuevamente la fuerza de Coriolis en acción. Cada vez que una corriente se desplaza en dirección del ecuador tiende a ser desviada hacia el lado poniente (en el hemisferio norte hacia la derecha de la corriente y en el hemisferio sur hacia la izquierda de la corriente). Desplazamientos hacia los polos muestran una tendencia inversa generando vórtices gigantes. En el hemisferio norte estos se mueven en el sentido de las manecillas del reloj
mientas que en el hemisferio sur lo hacen en el sentido contrario.
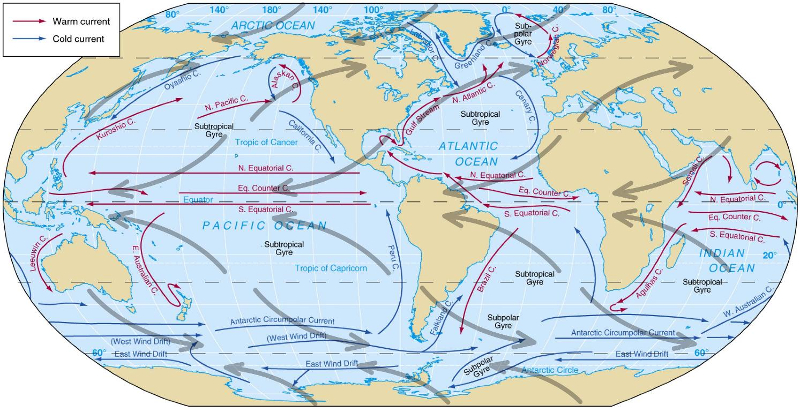
Circulación atmosférica y oceánica mostrando como la primera genera la segunda
Con esto queda también explicado de porque los continentes en su lado oriente son mas húmedos que en el lado poniente. En el lado oriental son bañados por aguas que alcanzaron el ecuador y tienen temperaturas masaltas y con ello pueden entregar mas calor y humedad al medio. En el lado poniente sin embargo las corrientes provienen de los polos y están a menor temperatura reduciéndose con ello la humedad que pueden aportar.
ID:(80, 0)
Corrientes marinas
Imagen 
Las corrientes marinas forman patrones de circulación propios de cada hemisferio y condicionado por los continentes que bordean los océanos respectivos.
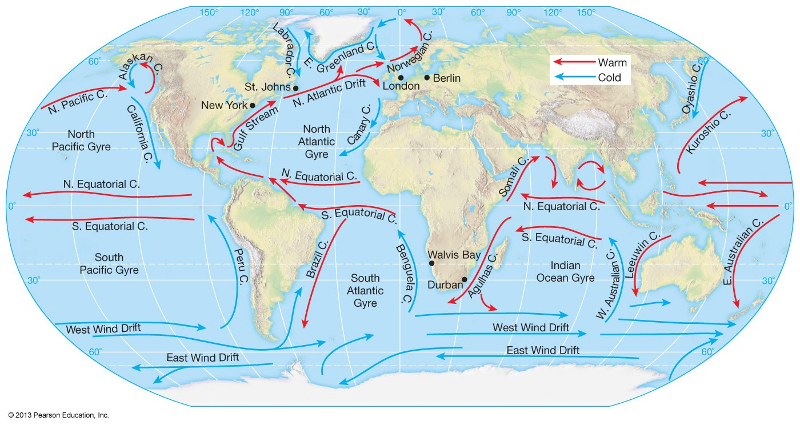
Circulación global, color indica si es caliente (rojo) o fria (azul)
En el hemisferio norte la corriente es en el sentido de la rotación del reloj (sentido negativo) mientras que en el hemisferio sur es en el sentido opuesto (sentido positivo).Esto se explica con la circulación del aire que es el principal motor de las corrientes marinas. Las masas de aire superficiales que convergen hacia el ecuador se retrasan con respecto de las masas en estas latitudes generando un desplazamiento paralelo al ecuador de oriente a poniente generan las respectivas corrientes marinas que luego circulan hacia los respectivos polos.
ID:(3144, 0)
Mareas por atracción y aceleración centrifuga
Descripción 
Después del viento es el sol y la luna los que contribuyen mas para impulsar las corrientes marinas generando lo que se denomina mareas. Estas provienen de la atracción gravitacional que sol y luna ejercen sobre la tierra.Existen dos tipos de influencias:- aquella que proviene de la atracción misma- aquella que proviene de la aceleración centrifuga al rotar la tierra en torno al centro de masa común tierra-sol o tierra-luna
ID:(79, 0)
Mareas lanares y solares
Imagen 
Las mareas son generadas tanto por el sol como la luna por lo que se habla de mareas lunares y solares.
Las mareas son máximas cuando luna y sol están alineados cuando la luna es llena o nueva siendo su periodicidad de 12 horas.
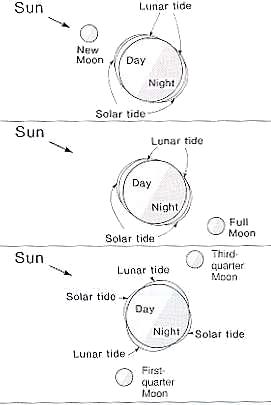
Si la luna están en cuarto menguante o cuarto creciente se encuentra en un radio luna tierra es perpendicular al radio sol tierra. En tal caso las mareas son menores y ocurren cada 6 horas alternándose una solar con una lunar.
ID:(3147, 0)
Salinidad en los mares
Imagen 
El océano tiene en promedio unos 34 g de sal por litro de agua. La sal
proviene tanto del agua de ríos como de procesos que ocurren en el fondo
del mar.
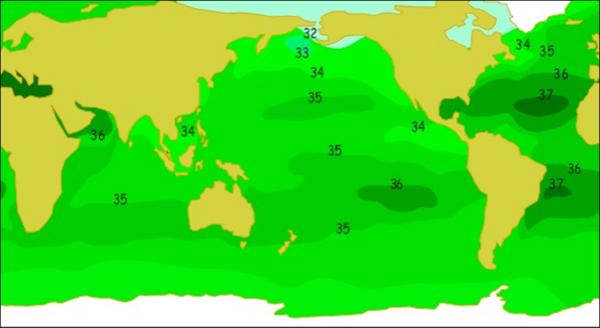
Salinidad en los mares
La importancia de la salinidad para la circulación del agua se debe a quezonas en que la densidad de la sal es mayor y/o la temperatura es menor sehunden desplazando a su vez agua e impulsando una corriente que mezclaaguas de distinta profundidad.
ID:(3145, 0)
Corrientes termohalinas
Imagen 
La sal contenida en el agua y la temperatura pueden llevar a que capas superiores del océano sean de mayor densidad y se hundan creando un flujo de mayor profundidad. Este transporta agua fría/caliente entre el océano atlándico, el indico y el pacifico por lo que se le llama también cincha transportadora global (ocean conveyor belt).
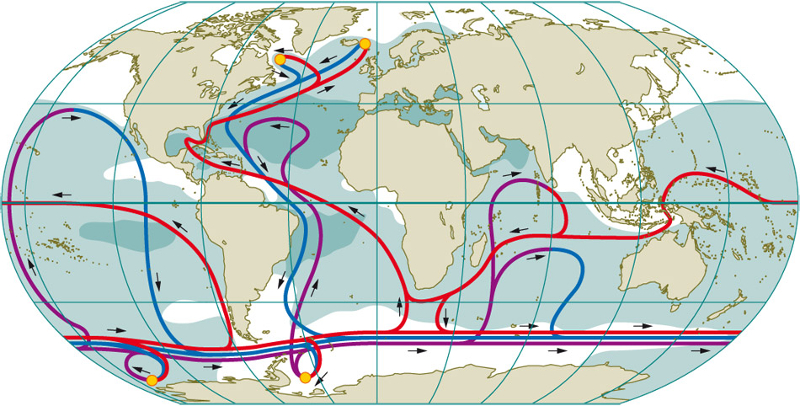
Cinta transportadora del oceano
Se presume que este es responsable del agua cálida que baña las costas de Europa con agua del caribe existiendo el temor que con los deshielo en el ártico se interrumpa o desplace cambiando en forma dramática el clima en Europa.
ID:(9242, 0)
Transporte de Ekman
Imagen 
Por efecto de la fuerza de Coriolis las aguas superficiales de corrientes que se desplazan en dirección del ecuador tienden a ser desvaídas hacia el poniente alejándose de los bordes costeros. Esto lleva a que aguas mas profundas deben acender en las zonas costeras para suplir este desplazamiento superficial.
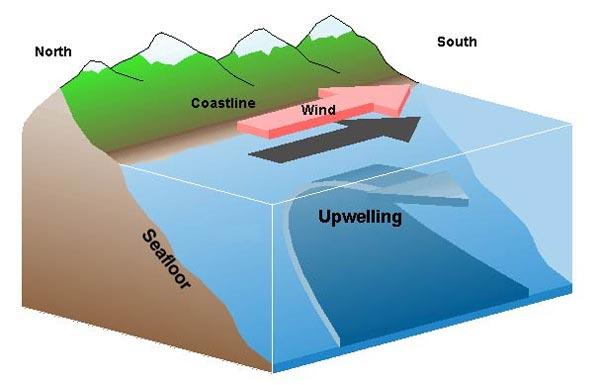
En este caso se mesura una corriente en el hemisferio norte circulando hacia el ecuador y desviándose mar afuera generando el transporte de Ekman.
Dichas corrientes acarrean aguas mas frías y con alta concentración de nutrientes a la superficie favoreciendo la vida marina costera.Este fenómeno, que se observa por ejemplo en las costas norte de Chile y en el Perú, se denomina transporte de Ekman.
ID:(3148, 0)
Dinámicas circulación marina
Modelo 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
El movimiento de la atm sfera es uno de los principales motores del movimiento de las masas de agua de los oc anos. Aun cuando no es un proceso demasiado eficiente. El viento logra que las capas del agua se desplacen a aproximadamente 2% de su velocidad. Sin embargo la inercia de la masa del agua hace que las corrientes persistan en el tiempo.
La circulaci n en mar se puede describir mediante grandes torbellinos que se forma en cada oc ano:

Circulaci n en el mar
Las circulaciones oce nicas tampoco son totalmente estables. Existen situaciones en que los torbellinos se desplazan como ha ocurrido con aquel que ba a las costas de Noruega con agua c lida del caribe creando inviernos mas fr os en las regiones escandinavas y en Europa en general.
(ID 77)
Si observamos los patrones que se dan en las corrientes oce nicas veremos nuevamente la fuerza de Coriolis en acci n. Cada vez que una corriente se desplaza en direcci n del ecuador tiende a ser desviada hacia el lado poniente (en el hemisferio norte hacia la derecha de la corriente y en el hemisferio sur hacia la izquierda de la corriente). Desplazamientos hacia los polos muestran una tendencia inversa generando v rtices gigantes. En el hemisferio norte estos se mueven en el sentido de las manecillas del reloj
mientas que en el hemisferio sur lo hacen en el sentido contrario.

Circulaci n atmosf rica y oce nica mostrando como la primera genera la segunda
Con esto queda tambi n explicado de porque los continentes en su lado oriente son mas h medos que en el lado poniente. En el lado oriental son ba ados por aguas que alcanzaron el ecuador y tienen temperaturas masaltas y con ello pueden entregar mas calor y humedad al medio. En el lado poniente sin embargo las corrientes provienen de los polos y est n a menor temperatura reduci ndose con ello la humedad que pueden aportar.
(ID 80)
Las corrientes marinas forman patrones de circulaci n propios de cada hemisferio y condicionado por los continentes que bordean los oc anos respectivos.

Circulaci n global, color indica si es caliente (rojo) o fria (azul)
En el hemisferio norte la corriente es en el sentido de la rotaci n del reloj (sentido negativo) mientras que en el hemisferio sur es en el sentido opuesto (sentido positivo).Esto se explica con la circulaci n del aire que es el principal motor de las corrientes marinas. Las masas de aire superficiales que convergen hacia el ecuador se retrasan con respecto de las masas en estas latitudes generando un desplazamiento paralelo al ecuador de oriente a poniente generan las respectivas corrientes marinas que luego circulan hacia los respectivos polos.
(ID 3144)
Despu s del viento es el sol y la luna los que contribuyen mas para impulsar las corrientes marinas generando lo que se denomina mareas. Estas provienen de la atracci n gravitacional que sol y luna ejercen sobre la tierra.Existen dos tipos de influencias:- aquella que proviene de la atracci n misma- aquella que proviene de la aceleraci n centrifuga al rotar la tierra en torno al centro de masa com n tierra-sol o tierra-luna
(ID 79)
Las mareas son generadas tanto por el sol como la luna por lo que se habla de mareas lunares y solares.
Las mareas son m ximas cuando luna y sol est n alineados cuando la luna es llena o nueva siendo su periodicidad de 12 horas.

Si la luna est n en cuarto menguante o cuarto creciente se encuentra en un radio luna tierra es perpendicular al radio sol tierra. En tal caso las mareas son menores y ocurren cada 6 horas altern ndose una solar con una lunar.
(ID 3147)
El oc ano tiene en promedio unos 34 g de sal por litro de agua. La sal
proviene tanto del agua de r os como de procesos que ocurren en el fondo
del mar.

Salinidad en los mares
La importancia de la salinidad para la circulaci n del agua se debe a quezonas en que la densidad de la sal es mayor y/o la temperatura es menor sehunden desplazando a su vez agua e impulsando una corriente que mezclaaguas de distinta profundidad.
(ID 3145)
La sal contenida en el agua y la temperatura pueden llevar a que capas superiores del oc ano sean de mayor densidad y se hundan creando un flujo de mayor profundidad. Este transporta agua fr a/caliente entre el oc ano atl ndico, el indico y el pacifico por lo que se le llama tambi n cincha transportadora global (ocean conveyor belt).

Cinta transportadora del oceano
Se presume que este es responsable del agua c lida que ba a las costas de Europa con agua del caribe existiendo el temor que con los deshielo en el rtico se interrumpa o desplace cambiando en forma dram tica el clima en Europa.
(ID 9242)
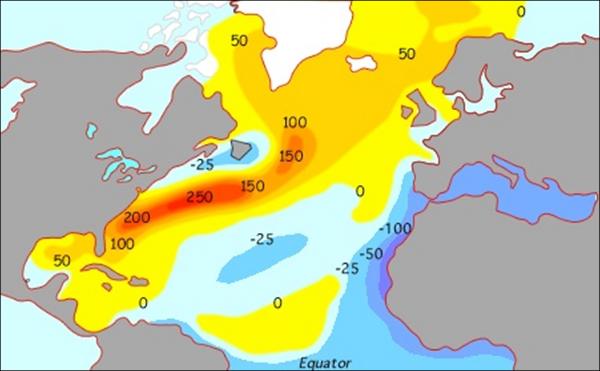
climate033
(ID 3146)
Por efecto de la fuerza de Coriolis las aguas superficiales de corrientes que se desplazan en direcci n del ecuador tienden a ser desva das hacia el poniente alej ndose de los bordes costeros. Esto lleva a que aguas mas profundas deben acender en las zonas costeras para suplir este desplazamiento superficial.

En este caso se mesura una corriente en el hemisferio norte circulando hacia el ecuador y desvi ndose mar afuera generando el transporte de Ekman.
Dichas corrientes acarrean aguas mas fr as y con alta concentraci n de nutrientes a la superficie favoreciendo la vida marina costera.Este fen meno, que se observa por ejemplo en las costas norte de Chile y en el Per , se denomina transporte de Ekman.
(ID 3148)
ID:(566, 0)
