Application in Microscopes
Storyboard 
The principle of the microscope is to capture the small image, which above as parallel beams and enlarge it with a biconvex lens to form a larger inverted real image.
ID:(299, 0)
Beam geometry in a lens, near object
Definition 
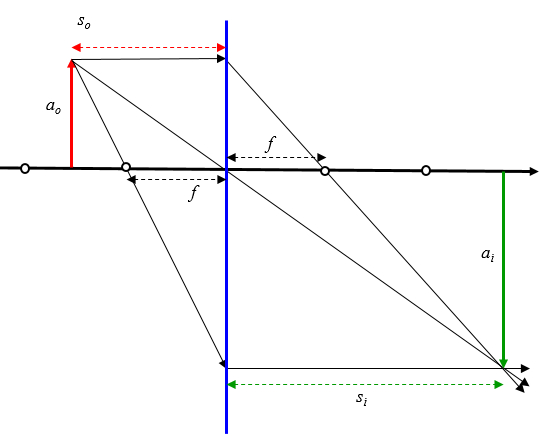
In the event that the object is closer to the lens than the focal point, the diagram to determine image size and position is somewhat more complex. In this case the beams must be
projected from where they would have reached the object that radiates them
within the projection the same rules as in a real beam must be followed
In this case it is enough to diagram the same three beams again:
- parallel to the optical axis is refracted by the focus
- via the focus is refracted parallel to the optical axis
- via the origin of the continuous optical axis in a straight line
and the image is obtained in the same way:
ID:(9783, 0)
Geometry of the Beams on a Lens
Note 
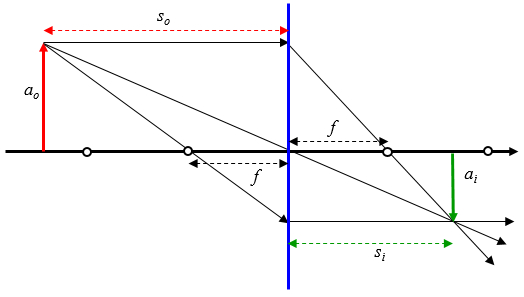
In the case of a biconvex lens a beam that reaches the lens
- parallel to the optical axis is refracted by the focus
- via the focus is refracted parallel to the optical axis
- via the origin of the continuous optical axis in a straight line
what in the case of an object at a distance greater than the photo corresponds to:
ID:(1856, 0)
Convex Lens
Quote 
A convex lens is a lens that refracts the parallel beam of light that strikes parallel through its focus:
ID:(1855, 0)
Concave Lens
Exercise 
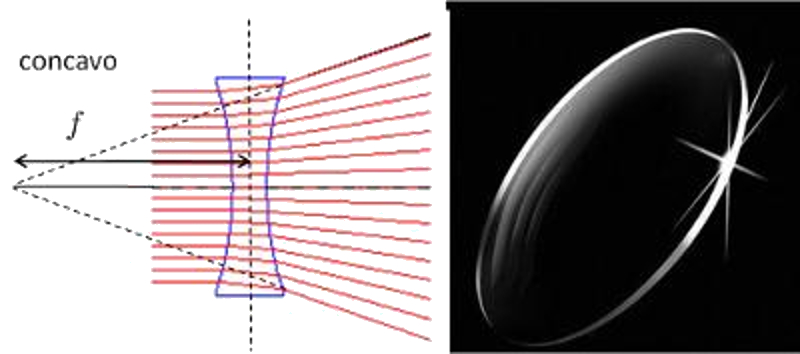
Convex lenses are thinner in their center widening towards the edges.

The light beams that have a parallel impact are scattered as if the light were emitted in the lens focus.
ID:(1854, 0)
Multiples lentes
Video 
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:

ID:(9465, 0)
Refraction depending on the color of light
Code 
The refractive index of glass can depend on the wavelength or frequency of light. In such cases, the glass is referred to as 'chromatic.' If it does not exhibit this property, it is called 'achromatic.'
The main issue with this property is that the focal point of a lens depends on the color of light. Therefore, an optical lens has the problem that if the eye can focus on one color, it will not be able to simultaneously focus on objects of other colors.

ID:(1626, 0)
Application in Microscopes
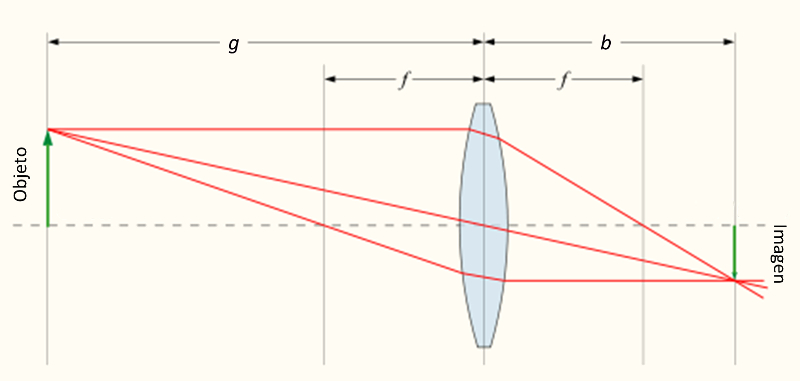
Description 
The principle of the microscope is to capture the small image, which above as parallel beams and enlarge it with a biconvex lens to form a larger inverted real image.
Variables
Calculations
Calculations
Equations
Una relaci n se puede armar con los tri ngulos del lado del objeto. En este caso la similitud nos permite escribir que el tama o del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relaci n de similitud de los tri ngulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
(ID 3347)
Examples
In the event that the object is closer to the lens than the focal point, the diagram to determine image size and position is somewhat more complex. In this case the beams must be
projected from where they would have reached the object that radiates them
within the projection the same rules as in a real beam must be followed
In this case it is enough to diagram the same three beams again:
- parallel to the optical axis is refracted by the focus
- via the focus is refracted parallel to the optical axis
- via the origin of the continuous optical axis in a straight line
and the image is obtained in the same way:

(ID 9783)
Correcci n con Lentes
(ID 1864)
In the case of a biconvex lens a beam that reaches the lens
- parallel to the optical axis is refracted by the focus
- via the focus is refracted parallel to the optical axis
- via the origin of the continuous optical axis in a straight line
what in the case of an object at a distance greater than the photo corresponds to:

(ID 1856)
A convex lens is a lens that refracts the parallel beam of light that strikes parallel through its focus:

(ID 1855)
Por similitud de los tri ngulos de los tama os del objeto y la imagen y las posiciones del objeto y foco permite por similitud de tri ngulos mostrar que:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
(ID 3347)
For any lens you can draw characteristic beams with which you can similarly show that the sizes of the object and the image are in the same proportion as their distances to the optical element (lens or mirror).
If the object has a size
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
(ID 3346)
Convex lenses are thinner in their center widening towards the edges.

The light beams that have a parallel impact are scattered as if the light were emitted in the lens focus.
(ID 1854)
Lente Bi-Concavo grueso
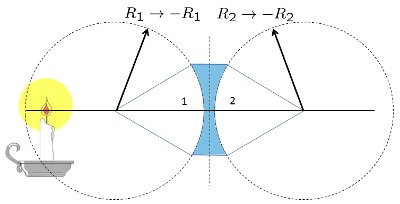
(ID 1858)
Lente Bi-Convexo grueso
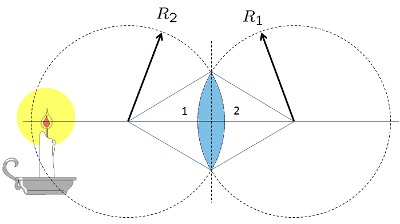
(ID 1857)
Lente Concavo-Convexo grueso
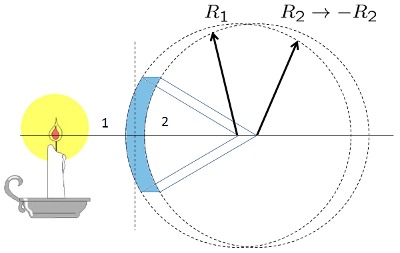
(ID 1859)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vsd} }=( n -1)\left(\displaystyle\frac{2}{ R }-\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
(ID 3432)
Lente Convexo-Concavo grueso
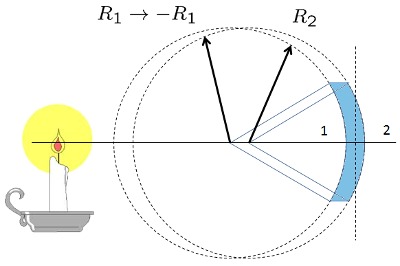
(ID 1860)
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracci n
| $\displaystyle\frac{1}{ f_{vvd} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }-\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
(ID 3348)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vcs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
(ID 3430)
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracci n
| $\displaystyle\frac{1}{ f_{vcs} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }-\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1) d }{ n R_1 R_2 }\right)$ |
(ID 3350)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{csd} }=-( n -1)\left(\displaystyle\frac{2}{ R } +\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
(ID 3431)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{cvs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
(ID 3429)
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracci n
| $\displaystyle\frac{1}{ f_{ccd} }=-( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
(ID 3349)
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:

(ID 9465)
Aqui va el applet ...
(ID 194)
The refractive index of glass can depend on the wavelength or frequency of light. In such cases, the glass is referred to as 'chromatic.' If it does not exhibit this property, it is called 'achromatic.'
The main issue with this property is that the focal point of a lens depends on the color of light. Therefore, an optical lens has the problem that if the eye can focus on one color, it will not be able to simultaneously focus on objects of other colors.

(ID 1626)
ID:(299, 0)
