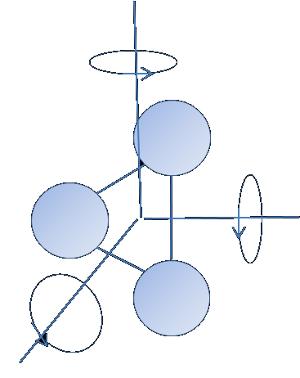
Energy of a particle with $f$ gardos freedom
Image 
Energy of a particle with
ID:(1960, 0)
Kinetic energy of molecules
Equation 
Since the particles can have a different speed we will work with average values. In such a case the average kinetic energy is
| $\langle\epsilon\rangle=\displaystyle\frac{1}{2}m\langle v^2\rangle$ |
is the average of the square of the speed.
ID:(3932, 0)
Molecules energy
Equation 
With the Boltzmann constant\\n\\n
$k_B=\displaystyle\frac{R}{N_A}$
\\n\\nand the energy per particle\\n\\n
$\langle\epsilon\rangle=\displaystyle\frac{3RT}{2N_A}$
you can write this as
| $\langle\epsilon\rangle=\displaystyle\frac{3}{2}kT$ |
ID:(3224, 0)
Energy of a particle with $f$ degrees of freedom
Equation 
If the particle has
| $\langle\epsilon\rangle=\displaystyle\frac{f}{2}kT$ |
ID:(3940, 0)
Energy of a particle system
Equation 
The energy
| $E=nN_A\langle\epsilon\rangle$ |
ID:(3933, 0)
