Utilisateur:
Contrôle du pas
Storyboard 
Le contrôle du tangage est le mécanisme qui permet de lever ou d'abaisser le nez de l'avion, ce qui est essentiel pour les mouvements de montée ou de descente. Ce contrôle est obtenu en générant une force de portance à l'aide des gouvernes de profondeur situées sur les petites ailes près de la queue de l'avion. Cette force crée un couple responsable de faire pivoter l'avion autour d'un axe imaginaire, parallèle aux ailes principales, appelé l'axe de tangage.
ID:(2113, 0)
Contrôle du pas
Concept
Pour incliner le nez de l'avion vers le haut ou vers le bas, on utilise les élévateurs. Les deux élévateurs sont utilisés de manière symétrique pour générer un effet symétrique a la force des ascenseurs ($F_e$). En les plaçant à l'arrière de l'avion, on obtient une ($$) plus grande efficacité en les situant près du centre de masse. Cela offre un contrôle suffisant pour relever ou abaisser le nez de l'avion.
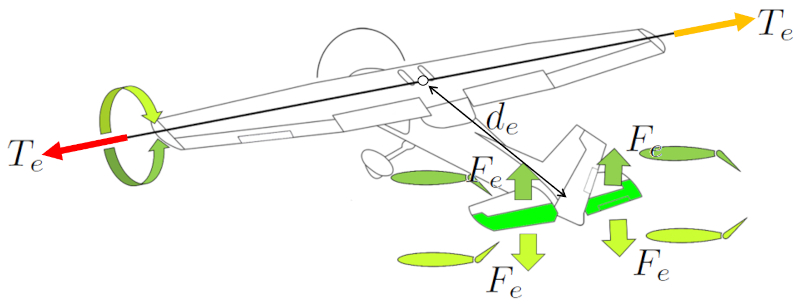
Sur les avions plus anciens, le contrôle des ailerons arrière s'effectue à l'aide d'un manche, où pousser vers l'avant fait descendre le nez de l'avion, et tirer vers l'arrière relève le nez. Sur les avions de la famille Airbus, ce contrôle s'effectue à l'aide d'un joystick.
Dans le cas des oiseaux, une solution similaire existe, bien que dans ce cas, la queue ne soit pas interrompue par un gouvernail.
ID:(15161, 0)
Masse de l'aile
Description
A masse de l'aile ($m_w$) peut être approximé comme le volume d'un parallélépipède rectangle multiplié par la densité de l'aéronef :
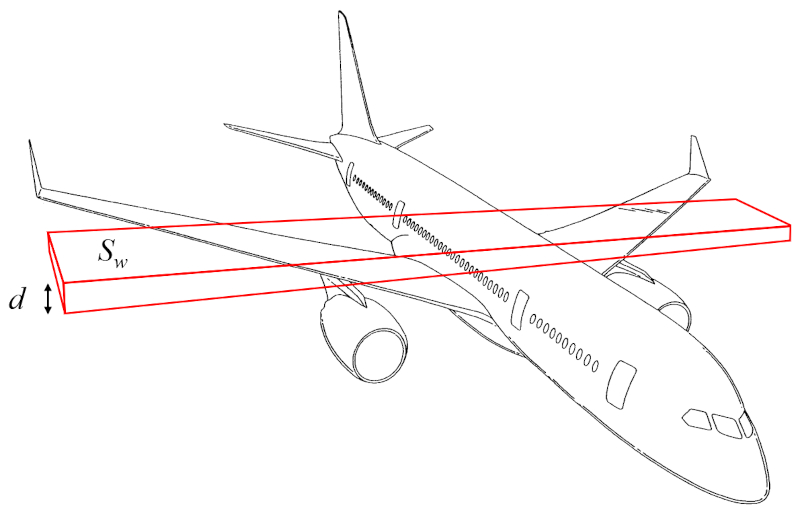
Le volume peut donc être calculé à partir de a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$).
Ainsi, a masse de l'aile ($m_w$) est déterminé en utilisant le densité du corps de l'avion ($\rho_a$), a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$), de la manière suivante :
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Moment d'inertie pour le tangage
Description
Le moment d'inertie de l'axe de l'aile ($I_e$) peut être approximé comme le moment d'inertie d'un cylindre représentant le corps de l'avion, tournant autour d'un axe perpendiculaire à l'axe du cylindre, parallèle aux ailes :
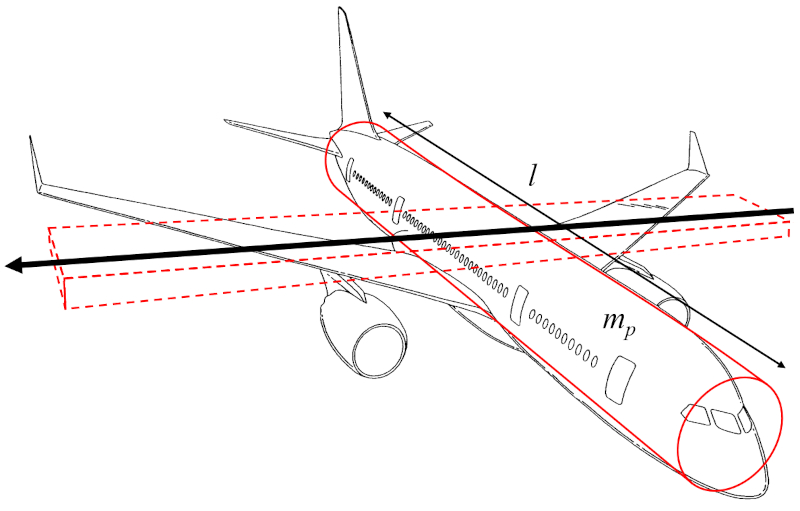
Étant donné que le largeur de l'aile ($w$) est beaucoup plus petit que le distance le long de l'aile ($l$), le terme impliquant $w^2$ peut être négligé, et l'on se concentre uniquement sur a masse corporelle de l'avion ($m_p$) et le terme le distance le long de l'aile ($l$) au carré.
Par conséquent, le moment d'inertie de l'axe de l'aile ($I_e$) se calcule à partir de a masse corporelle de l'avion ($m_p$) et le distance le long de l'aile ($l$), comme suit :
 $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15991, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ C_L = c \alpha $
C_L = c * alpha
$ d_e = \displaystyle\frac{ l }{2}$
d_e = l /2
$ F_L =\displaystyle\frac{1}{2} \rho S_e C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ I_e = \displaystyle\frac{1}{12} m_p l ^2$
I_e = m_p * l ^2/12
$ m_p = \rho_a S_p l $
m_p = rha_a * S_p * l
$ T_e = d_e F_L $
T_e = d_e * F_e
$ T_e = I_e \alpha_e $
T_e = I_e * alpha_e
ID:(15172, 0)
Force générée par le tangage
Équation
| $ T_e = d_e F_L $ |
| $ T_e = d_e F_e $ |
ID:(15163, 0)
Couple de pas
Équation
| $ T_e = I_e \alpha_e $ |
ID:(15166, 0)
Soulevez
Équation
Pour générer une pression plus élevée en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilisé pour corriger le manque de conservation de la densité d'énergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut être estimée en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) grâce à la formule suivante :
| $ F_L =\displaystyle\frac{1}{2} \rho S_e C_L v ^2$ |
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous considérons a surface génératrice de portance ($S_w$), défini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
et pour le coefficient de portance ($C_L$), défini comme
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
nous obtenons
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Constante de levage
Équation
À partir de mesures, il est conclu que le coefficient de portance $C_L$ est proportionnel à l'angle d\'attaque $\alpha$:
| $ C_L = c \alpha $ |
Après un certain angle, la courbe diminue jusqu\'à atteindre zéro. Cela est dû au fait que au-delà de cet angle critique, les tourbillons recouvrent entièrement la surface supérieure de l\'aile, ce qui entraîne une perte de portance. Ce phénomène est appelé \"décrochage\" ou \"décrochage aérodynamique\".
ID:(4441, 0)
Moment d'inertie pour le tangage
Équation
A masse de l'aile ($m_w$) est calculé à partir de a masse corporelle de l'avion ($m_p$) et ($$)10333
| $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15987, 0)
Masse corporelle de l'avion
Équation
A masse corporelle de l'avion ($m_p$) est calculé à partir de le densité du corps de l'avion ($\rho_a$), le profil total de l'objet ($S_p$) et le distance le long de l'aile ($l$), comme suit :
| $ m_p = \rho_a S_p l $ |
ID:(15985, 0)
Bras de force pour ascenseurs
Équation
A distance centre de masse et ascenseurs ($d_e$) est défini comme la moitié de le distance le long de l'aile ($l$), exprimé comme suit :
| $ d_e = \displaystyle\frac{ l }{2}$ |
ID:(15994, 0)