La ley de Charles establece que el volumen de un gas es directamente proporcional a su temperatura cuando la presi n se mantiene constante. Esto significa que, a medida que la temperatura de un gas aumenta, su volumen tambi n aumenta, siempre que la presi n permanezca igual. De manera inversa, si la temperatura disminuye, el volumen disminuye. Esta relaci n es fundamental para entender el comportamiento de los gases y se observa com nmente al calentar o enfriar un gas en un contenedor flexible, como un globo, donde el cambio de temperatura resulta en un cambio notable de volumen.

simulation

La generaci n de la presión ($p$) ocurre cuando las part culas de gas chocan con la superficie del contenedor de gas. Cada choque transmite un momento igual al doble de la masa de la partícula ($m$) por la velocidad media de una partícula ($\bar{v}$). Adem s, es importante considerar el flujo de part culas hacia la superficie, que depende de la concentración de particulas ($c_n$) pero tambi n de la velocidad media de una partícula ($\bar{v}$) con el que se desplazan. Por lo tanto,

$p \propto c_n v \cdot m v = c_n m v^2$

El flujo de part culas y la transmisi n del momento se representan en la siguiente gr fica:

image

Dado que la masa de la partícula ($m$) por la velocidad media de una partícula ($\bar{v}$) al cuadrado es proporcional a la energ a, y esta a la temperatura absoluta ($T$),

$mv^2 \propto E \propto T$

y, dado que el número de partículas ($N$) es constante, la concentración de particulas ($c_n$) es inversamente proporcional a el volumen ($V$):

$c_n \propto \displaystyle\frac{1}{V}$

Dado que la presión ($p$) es constante, tenemos:

$p \propto \displaystyle\frac{T}{V}$

lo que implica:

$V \propto T$

La temperatura corresponde a la cantidad de energ a t rmica (movimiento molecular) contenida en un cuerpo.

Dado que la energ a siempre es positiva, escalas de temperatura como Celsius y Fahrenheit, que pueden tomar valores negativos, pueden parecer poco intuitivas. Sin embargo, la relaci n entre energ a y temperatura lleva a la conclusi n de que debe existir una temperatura m nima, conocida como temperatura cero absoluta, en la cual la energ a de un sistema de part culas es nula.

Adem s, en 1802, Gay-Lussac observ que en los gases existe una relaci n proporcional entre el volumen y la temperatura. Esta proporcionalidad implica que un gas alcanzar a un volumen nulo a una temperatura de -273.15 grados Celsius (seg n mediciones actuales), lo que se conoce como cero absoluto de temperatura:

image

Esto implica que existe una escala de temperatura absoluta, conocida como la escala de grados Kelvin. Otras escalas, como las temperaturas $t$ en grados Celsius o Fahrenheit, pueden convertirse a :

Celsius:

$T = 273.15 + t$

Fahrenheit:

$T = 255.37 + \displaystyle\frac{5}{9} t$

La diferencia de temperatura en grados Celsius ($\Delta t$) en combinaci n con la temperatura en grados Celsius en estado 1 ($t_1$) y la temperatura en grados Celsius en estado 2 ($t_2$) da como resultado:

$\Delta t = t_2 - t_1$

Si representamos ambas temperaturas en grados Kelvin, obtenemos que la temperatura en estado 1 ($T_1$) es igual a:

$T_1 = t_1 + 273.15 , \text{K}$

y la temperatura en estado 2 ($T_2$) es igual a:

$T_2 = t_2 + 273.15 , \text{K}$

Por lo tanto, la diferencia de temperaturas en grados Kelvin, denotada como la diferencia de temperatura ($\Delta T$), se calcula como:

$\Delta T=T_2-T_1=t_2-t_1=\Delta t$

Esto implica que:

equation=4380

Lo cual significa que la diferencia entre las temperaturas en grados Celsius y Kelvin es constante.

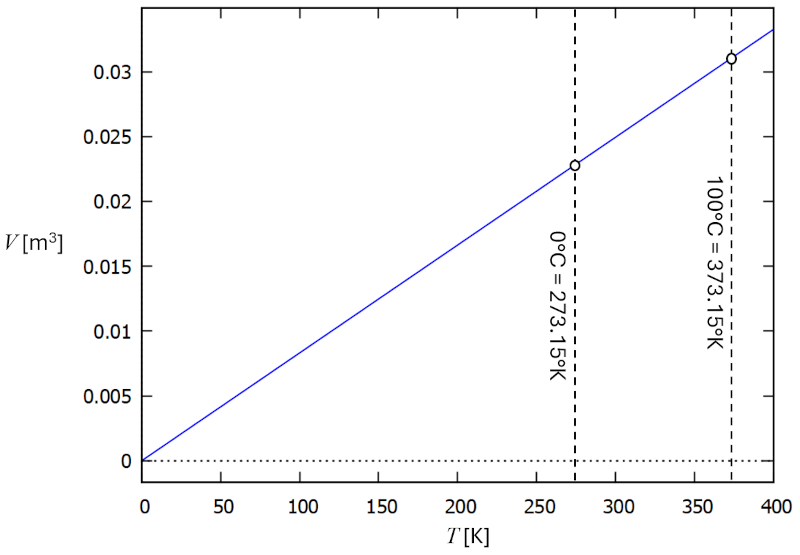
En un gas, si se mantiene constante la presión ($p$) y el número de partículas ($N$), se observa que el volumen ($V$) y la temperatura absoluta ($T$) var an de forma proporcional. Cuando el volumen ($V$) disminuye, la temperatura absoluta ($T$) tambi n disminuye, y viceversa,

$V \propto T$

como se ilustra en el siguiente gr fico:

image

La ley de Charles [1] establece que, manteniendo la presión ($p$) y el número de partículas ($N$) constantes, el volumen ($V$) y la temperatura absoluta ($T$) son directamente proporcionales.

Esto se puede expresar con la constante de la ley de Charles ($C_c$) de la siguiente manera:

equation=583

[1] "Sur la dilataci n de los gases y vapores" (Sobre la expansi n de gases y vapores), Jacques Charles, Academia de Ciencias de Francia (1787)

Jacques Charles, nacido el 12 de noviembre de 1746 y fallecido el 7 de abril de 1823, fue un f sico, inventor y aeronauta franc s. Es conocido principalmente por su trabajo pionero en el campo de la aeron utica y por sus descubrimientos relacionados con el comportamiento de los gases. En 1783, realiz el primer vuelo tripulado en globo lleno de hidr geno, junto con el qu mico Nicolas-Louis Robert. Este exitoso vuelo marc un hito importante en la historia de la aviaci n. Charles tambi n realiz importantes contribuciones en la comprensi n de las leyes de los gases, incluida la Ley de Charles, que describe la relaci n entre el volumen y la temperatura de un gas a presi n constante.

Nota: La ley de Charles se hizo p blica por Joseph Louis Gay-Lussac, quien se la atribuy a Jacques Charles citando un art culo no publicado.

image

La ley de Charles establece que, con la presión ($p$) constante, se cumple que la proporci n de el volumen ($V$) con la temperatura absoluta ($T$) es igual a la constante de la ley de Charles ($C_c$):

equation=583

Esto significa que si un gas pasa de un estado inicial (el volumen en estado i ($V_i$) y la temperatura en estado inicial ($T_i$)) a un estado final (el volumen en estado f ($V_f$) y la temperatura en estado final ($T_f$)), manteniendo la presión ($p$) constante, debe siempre cumplir la ley de Charles:

$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$

Por lo tanto, se tiene que:

equation=3492

En un proceso isob rico en el que el contenido permanece constante, si el volumen en estado i ($V_i$), la temperatura en estado final ($T_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$) est n relacionados por:

equation=3492

Entonces, podemos introducir la densidad ($\rho$), que, junto con la masa ($M$) y el volumen ($V$), satisface:

equation=3704

Esto nos lleva a la densidad en estado i ($\rho_i$) y la densidad en estado f ($\rho_f$) como:

equation=8835

model

La ley de Charles establece una relaci n entre el volumen ($V$) y la temperatura absoluta ($T$), indicando que su proporcion es igual a la constante de la ley de Charles ($C_c$), de la siguiente manera:

kyon

La ley de Charles establece una relaci n entre el volumen ($V$) y la temperatura absoluta ($T$), indicando que su proporcion es igual a la constante de la ley de Charles ($C_c$), de la siguiente manera:

kyon

Si un gas pasa de un estado inicial (i) a un estado final (f) con la presión ($p$) constante, se cumple que para el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):

kyon

La densidad ($\rho$) se define como la relaci n entre la masa ($M$) y el volumen ($V$), que se expresa como:

kyon

Esta propiedad es espec fica del material en cuesti n.

La densidad ($\rho$) se define como la relaci n entre la masa ($M$) y el volumen ($V$), que se expresa como:

kyon

Esta propiedad es espec fica del material en cuesti n.

Para los estados inicial (la densidad en estado i ($\rho_i$), el volumen en estado i ($V_i$)) y final (la densidad en estado f ($\rho_f$), el volumen en estado f ($V_f$)), la ley de Charles se obtiene como sigue:

kyon