Interceptar em aceleração constante
Storyboard 
Os objetos podem se interceptar quando coincidem em posição no mesmo momento. Para isso, devem se deslocar a partir de seus respectivos pontos e velocidades iniciais com acelerações que lhes permitam coincidir em posição e tempo ao final da jornada.
ID:(1412, 0)
Variação na velocidade e duração
Imagem 
Em um cenário de movimento envolvendo dois corpos, o primeiro altera sua velocidade em la diferença de velocidade do primeiro corpo ($\Delta v_1$) durante uma tempo de percurso do primeiro objeto ($\Delta t_1$) com la primeira aceleração corporal ($a_1$).
| $ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$ |
Posteriormente, o segundo corpo avança, alterando sua velocidade em la segunda diferença de velocidade corporal ($\Delta v_2$) durante um intervalo de tempo de la tempo de percurso do segundo objeto ($\Delta t_2$) com la aceleração do segundo corpo ($a_2$).
| $ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$ |
Quando representado graficamente, obtemos um diagrama de velocidade-tempo conforme mostrado abaixo:
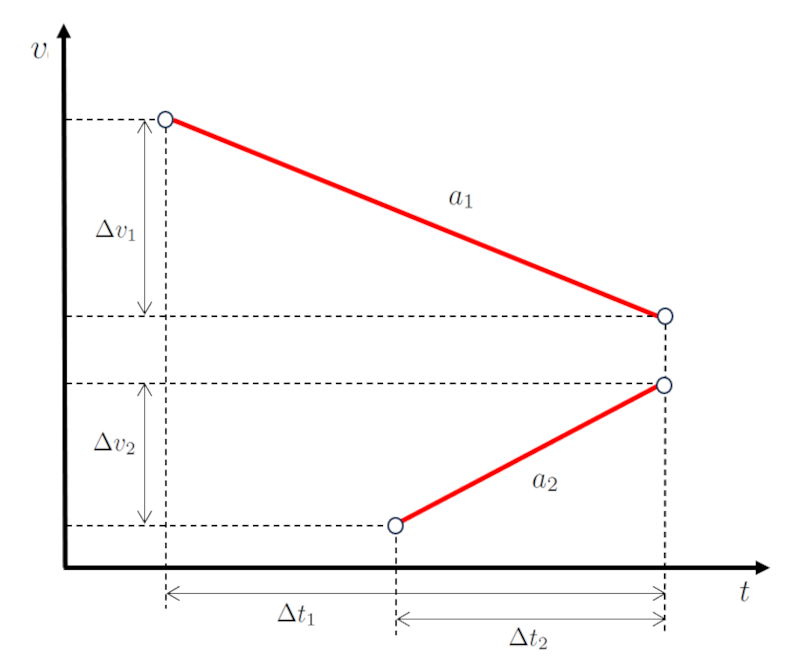
A chave aqui é que os valores la diferença de velocidade do primeiro corpo ($\Delta v_1$) e la segunda diferença de velocidade corporal ($\Delta v_2$), e os valores la tempo de percurso do primeiro objeto ($\Delta t_1$) e la tempo de percurso do segundo objeto ($\Delta t_2$), são tais que ambos os corpos coincidem no lugar e no tempo.
ID:(12512, 0)
Velocidade e tempos de interseção
Nota 
No caso de dois corpos, o movimento do primeiro pode ser descrito por uma função que envolve os pontos o tempo inicial do primeiro objeto ($t_1$), o tempo de interseção ($t$), la velocidade inicial do primeiro corpo ($v_{01}$) e la velocidade final do primeiro corpo ($v_1$), representada por uma reta com uma inclinação de la primeira aceleração corporal ($a_1$):
| $ v_1 = v_{01} + a_1 ( t - t_1 )$ |
Para o movimento do segundo corpo, definido pelos pontos la velocidade inicial do segundo corpo ($v_{02}$), la velocidade final do segundo corpo ($v_2$), o tempo inicial do segundo objeto ($t_2$) e o tempo de interseção ($t$), é empregada uma segunda reta com uma inclinação de la aceleração do segundo corpo ($a_2$):
| $ v_2 = v_{02} + a_2 ( t - t_2 )$ |
Isso é representado como:

ID:(12515, 0)
Evolução da posição dos corpos
Citar 
No caso de um movimento de dois corpos, a posição onde a trajetória do primeiro termina coincide com a do segundo corpo em la posição de interseção ($s$).
Da mesma forma, o tempo em que a trajetória do primeiro termina coincide com a do segundo corpo em o tempo de interseção ($t$).
Para o primeiro corpo, la posição de interseção ($s$) depende de la posição inicial do primeiro objeto ($s_1$), la velocidade inicial do primeiro corpo ($v_{01}$), la primeira aceleração corporal ($a_1$), o tempo inicial do primeiro objeto ($t_1$), conforme:
| $ s = s_1 + v_{01} ( t - t_1 )+\displaystyle\frac{1}{2} a_1 ( t - t_1 )^2$ |
Enquanto para o segundo corpo, la posição de interseção ($s$) depende de la posição inicial do segundo objeto ($s_2$), la velocidade inicial do segundo corpo ($v_{02}$), la aceleração do segundo corpo ($a_2$), o tempo inicial do segundo objeto ($t_2$), conforme:
| $ s = s_2 + v_{02} ( t - t_2 )+\displaystyle\frac{1}{2} a_2 ( t - t_2 )^2$ |
Isso é representado como:
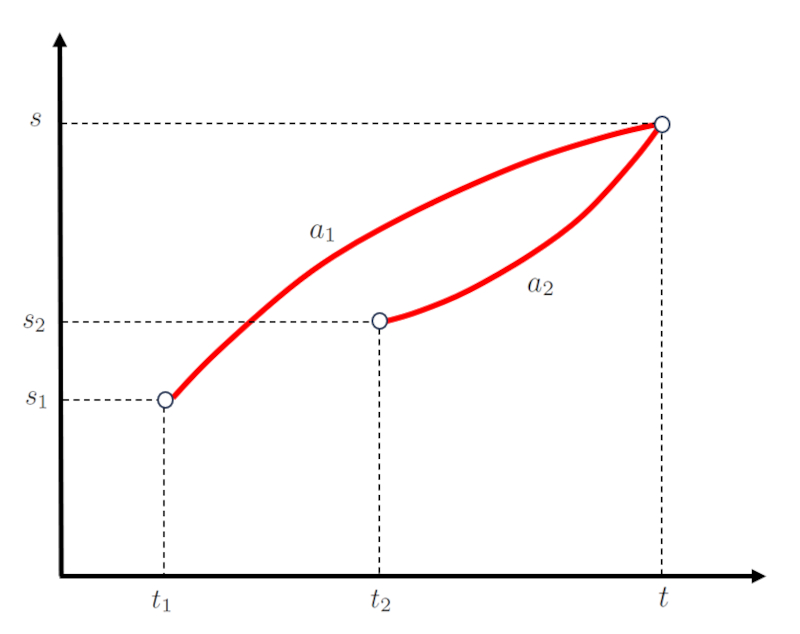
ID:(12513, 0)
Interceptar em aceleração constante
Storyboard 
Os objetos podem se interceptar quando coincidem em posição no mesmo momento. Para isso, devem se deslocar a partir de seus respectivos pontos e velocidades iniciais com acelerações que lhes permitam coincidir em posição e tempo ao final da jornada.
Variáveis
Cálculos
Cálculos
Equações
No caso em que la aceleração constante ($a_0$) igual a la aceleração média ($\bar{a}$), ser igual a
Portanto, se considerarmos la diferença de velocidade ($\Delta v$) como
e o tempo decorrido ($\Delta t$) como
temos que a equa o para la aceleração constante ($a_0$)
pode ser escrita como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
portanto, ao rearranjarmos, obtemos
No caso em que la aceleração constante ($a_0$) igual a la aceleração média ($\bar{a}$), ser igual a
Portanto, se considerarmos la diferença de velocidade ($\Delta v$) como
e o tempo decorrido ($\Delta t$) como
temos que a equa o para la aceleração constante ($a_0$)
pode ser escrita como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
portanto, ao rearranjarmos, obtemos
No caso de la aceleração constante ($a_0$), la velocidade ($v$) em fun o de o tempo ($t$) uma reta que passa por o tempo inicial ($t_0$) e la velocidade inicial ($v_0$) da forma:
Como la distância percorrida em um tempo ($\Delta s$) igual rea sob a curva velocidade-tempo, podemos somar a contribui o do ret ngulo:
$v_0(t-t_0)$
e do tri ngulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Com isso, obtemos com la posição ($s$) e la velocidade ($s_0$):
Resultando em:
No caso de la aceleração constante ($a_0$), la velocidade ($v$) em fun o de o tempo ($t$) uma reta que passa por o tempo inicial ($t_0$) e la velocidade inicial ($v_0$) da forma:
Como la distância percorrida em um tempo ($\Delta s$) igual rea sob a curva velocidade-tempo, podemos somar a contribui o do ret ngulo:
$v_0(t-t_0)$
e do tri ngulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Com isso, obtemos com la posição ($s$) e la velocidade ($s_0$):
Resultando em:
Se resolvermos as equa es para o tempo ($t$) e o tempo inicial ($t_0$) na equa o de la velocidade ($v$), que depende de la velocidade inicial ($v_0$) e la aceleração constante ($a_0$):
obtemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Ent o, substituindo essa express o na equa o de la posição ($s$) com la velocidade ($s_0$):
obtemos uma express o do caminho percorrido em fun o da velocidade:
Se resolvermos as equa es para o tempo ($t$) e o tempo inicial ($t_0$) na equa o de la velocidade ($v$), que depende de la velocidade inicial ($v_0$) e la aceleração constante ($a_0$):
obtemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Ent o, substituindo essa express o na equa o de la posição ($s$) com la velocidade ($s_0$):
obtemos uma express o do caminho percorrido em fun o da velocidade:
A defini o de la aceleração média ($\bar{a}$) considerada como a rela o entre la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$). Ou seja,
e
A rela o entre ambos definida como la aceleração centrífuga ($a_c$)
dentro desse intervalo de tempo.
A defini o de la aceleração média ($\bar{a}$) considerada como a rela o entre la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$). Ou seja,
e
A rela o entre ambos definida como la aceleração centrífuga ($a_c$)
dentro desse intervalo de tempo.
Exemplos
Em um cen rio de movimento envolvendo dois corpos, o primeiro altera sua velocidade em la diferença de velocidade do primeiro corpo ($\Delta v_1$) durante uma tempo de percurso do primeiro objeto ($\Delta t_1$) com la primeira aceleração corporal ($a_1$).
Posteriormente, o segundo corpo avan a, alterando sua velocidade em la segunda diferença de velocidade corporal ($\Delta v_2$) durante um intervalo de tempo de la tempo de percurso do segundo objeto ($\Delta t_2$) com la aceleração do segundo corpo ($a_2$).
Quando representado graficamente, obtemos um diagrama de velocidade-tempo conforme mostrado abaixo:
A chave aqui que os valores la diferença de velocidade do primeiro corpo ($\Delta v_1$) e la segunda diferença de velocidade corporal ($\Delta v_2$), e os valores la tempo de percurso do primeiro objeto ($\Delta t_1$) e la tempo de percurso do segundo objeto ($\Delta t_2$), s o tais que ambos os corpos coincidem no lugar e no tempo.
No caso de dois corpos, o movimento do primeiro pode ser descrito por uma fun o que envolve os pontos o tempo inicial do primeiro objeto ($t_1$), o tempo de interseção ($t$), la velocidade inicial do primeiro corpo ($v_{01}$) e la velocidade final do primeiro corpo ($v_1$), representada por uma reta com uma inclina o de la primeira aceleração corporal ($a_1$):
Para o movimento do segundo corpo, definido pelos pontos la velocidade inicial do segundo corpo ($v_{02}$), la velocidade final do segundo corpo ($v_2$), o tempo inicial do segundo objeto ($t_2$) e o tempo de interseção ($t$), empregada uma segunda reta com uma inclina o de la aceleração do segundo corpo ($a_2$):
Isso representado como:
No caso de um movimento de dois corpos, a posi o onde a trajet ria do primeiro termina coincide com a do segundo corpo em la posição de interseção ($s$).
Da mesma forma, o tempo em que a trajet ria do primeiro termina coincide com a do segundo corpo em o tempo de interseção ($t$).
Para o primeiro corpo, la posição de interseção ($s$) depende de la posição inicial do primeiro objeto ($s_1$), la velocidade inicial do primeiro corpo ($v_{01}$), la primeira aceleração corporal ($a_1$), o tempo inicial do primeiro objeto ($t_1$), conforme:
Enquanto para o segundo corpo, la posição de interseção ($s$) depende de la posição inicial do segundo objeto ($s_2$), la velocidade inicial do segundo corpo ($v_{02}$), la aceleração do segundo corpo ($a_2$), o tempo inicial do segundo objeto ($t_2$), conforme:
Isso representado como:
A acelera o corresponde varia o da velocidade por unidade de tempo.
Portanto, necess rio definir la diferença de velocidade ($\Delta v$) em fun o de la velocidade ($v$) e la velocidade inicial ($v_0$) como:
A acelera o corresponde varia o da velocidade por unidade de tempo.
Portanto, necess rio definir la diferença de velocidade ($\Delta v$) em fun o de la velocidade ($v$) e la velocidade inicial ($v_0$) como:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
A propor o na qual a varia o da velocidade ao longo do tempo definida como la aceleração média ($\bar{a}$). Para medi-la, necess rio observar la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$).
Um m todo comum para medir a acelera o m dia envolve o uso de uma l mpada estrobosc pica que ilumina o objeto em intervalos definidos. Ao tirar uma fotografia, pode-se determinar a dist ncia percorrida pelo objeto nesse tempo. Calculando duas velocidades consecutivas, pode-se determinar sua varia o e, com o tempo decorrido entre as fotos, a acelera o m dia.
A equa o que descreve a acelera o m dia a seguinte:
importante notar que a acelera o m dia uma estimativa da acelera o real.
O principal problema que se a acelera o variar durante o tempo decorrido, o valor da acelera o m dia pode diferir muito da acelera o m dia real.
Portanto, a chave
Determinar a acelera o em um per odo de tempo suficientemente curto para minimizar a varia o.
A propor o na qual a varia o da velocidade ao longo do tempo definida como la aceleração média ($\bar{a}$). Para medi-la, necess rio observar la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$).
Um m todo comum para medir a acelera o m dia envolve o uso de uma l mpada estrobosc pica que ilumina o objeto em intervalos definidos. Ao tirar uma fotografia, pode-se determinar a dist ncia percorrida pelo objeto nesse tempo. Calculando duas velocidades consecutivas, pode-se determinar sua varia o e, com o tempo decorrido entre as fotos, a acelera o m dia.
A equa o que descreve a acelera o m dia a seguinte:
importante notar que a acelera o m dia uma estimativa da acelera o real.
O principal problema que se a acelera o variar durante o tempo decorrido, o valor da acelera o m dia pode diferir muito da acelera o m dia real.
Portanto, a chave
Determinar a acelera o em um per odo de tempo suficientemente curto para minimizar a varia o.
Se la aceleração constante ($a_0$), ent o la aceleração média ($\bar{a}$) igual ao valor da acelera o, ou seja,
Neste caso, la velocidade ($v$) como fun o de o tempo ($t$) pode ser calculada lembrando que est associada diferen a entre la velocidade ($v$) e la velocidade inicial ($v_0$), bem como o tempo ($t$) e o tempo inicial ($t_0$).
Dessa forma, a equa o representa uma linha reta no espa o velocidade-tempo.
Se la aceleração constante ($a_0$), ent o la aceleração média ($\bar{a}$) igual ao valor da acelera o, ou seja,
Neste caso, la velocidade ($v$) como fun o de o tempo ($t$) pode ser calculada lembrando que est associada diferen a entre la velocidade ($v$) e la velocidade inicial ($v_0$), bem como o tempo ($t$) e o tempo inicial ($t_0$).
Dessa forma, a equa o representa uma linha reta no espa o velocidade-tempo.
No caso de uma aceleração constante ($a_0$), la velocidade ($v$) varia de forma linear com o tempo ($t$), usando la velocidade inicial ($v_0$) e o tempo inicial ($t_0$):
Portanto, podemos calcular a rea sob essa reta, o que nos leva a la distância percorrida em um tempo ($\Delta s$), permitindo calcular la posição ($s$) com la velocidade ($s_0$), resultando em:
Isso corresponde forma geral de uma par bola.
No caso de uma aceleração constante ($a_0$), la velocidade ($v$) varia de forma linear com o tempo ($t$), usando la velocidade inicial ($v_0$) e o tempo inicial ($t_0$):
Portanto, podemos calcular a rea sob essa reta, o que nos leva a la distância percorrida em um tempo ($\Delta s$), permitindo calcular la posição ($s$) com la velocidade ($s_0$), resultando em:
Isso corresponde forma geral de uma par bola.
No caso de uma acelera o constante, podemos calcular la posição ($s$) a partir de la velocidade ($s_0$), la velocidade inicial ($v_0$), o tempo ($t$) e o tempo inicial ($t_0$) com a seguinte equa o:
Isso nos permite calcular a rela o entre a dist ncia percorrida durante a acelera o/desacelera o em fun o da mudan a de velocidade:
No caso de uma acelera o constante, podemos calcular la posição ($s$) a partir de la velocidade ($s_0$), la velocidade inicial ($v_0$), o tempo ($t$) e o tempo inicial ($t_0$) com a seguinte equa o:
Isso nos permite calcular a rela o entre a dist ncia percorrida durante a acelera o/desacelera o em fun o da mudan a de velocidade:
Podemos calcular la distância percorrida em um tempo ($\Delta s$) a partir de la velocidade ($s_0$) y la posição ($s$) usando a seguinte equa o:
Podemos calcular la distância percorrida em um tempo ($\Delta s$) a partir de la velocidade ($s_0$) y la posição ($s$) usando a seguinte equa o:
ID:(1412, 0)
